Robin Wylie - University of Leeds MRes "Physics of the Earth and Atmosphere" 2009/10

This tutorial has two aims: 1. To provide an overview of the technique and application of Seismic Noise Interferometry (SNI); and 2. To act as a manual for the practical implementation of SNI by demonstrating the processing steps which I employ in my MRes research, and providing examples of results. 

1. Background  

In seismology, the term "noise" refers to ground motion which is recorded in the absence of an identifiable source of seismic energy, such as an earthquake. The continuous interaction of low frequency (<1Hz) oceanic surface waves (swells) with the Earth's crust is the main cause of natural ambient noise  and is observed globally (Aki and Richards). In most seismic applications steps are taken to remove the effect of the ambient noise, as it acts to obscure other seismic signals which are traditionally used to infer information about the subsurface; usually the P-, S-, and surface waves generated by earthquakes or man-made sources.

In recent years however it has emerged that ambient noise is far from useless: it has been demonstrated theoretically and in practice that by applying the simple operation of cross-correlation (see section 1.2) to pairs of ambient noise records made at the Earth's surface, useful information about the seismic properties of the subsurface can be obtained: this process is known as Seismic noise interferometry (SNI).

In a 2004 paper (Wapenaar), it was demonstrated that, in any medium, the cross-correlation of recordings of a random wavefield, made at different locations on a free-surface, theoretically synthesises the seismic energy that would be recorded at one of the receiver locations if there had been an impulsive seismic source at the other. This result is often given in terms of a Greens function (see section 1.1). Oceanic noise becomes random when averaged over a sufficient time period, and in the past few years it has been practically shown that interstation Greens functions can indeed be obtained by cross-correlating pairs of ambient noise records, presenting geophysicists with a powerful new tool for studying the subsurface.

1.1 Green's functions

In seismology, the Greens function (GF) between a pair of locations on or within the Earth's surface, describes the seismic energy which would result at one if there was an impulsive seismic source at the other. In other words, the GF describes the effect of the medium between the two locations on an impulsive source, and contains traveltime and waveform information about all the seismic phases that pass between the two locations. The complexities of the real earth and recording restrictions preclude computation of complete GFs, however a GF can reasonably be thought of as the seismogram which would be recorded at some location in response to a source at another (fig. 1).

Figure 1. Representation of a Greens function, which describes the energy which would be recorded at a receiver (bottom) in response to an impulsive source (top). Black arrows indicate the direction of wave propagation

1.2 Cross-correlation

Cross-correlation is an operation which measures the similarity of two waveforms in time by identifying the time lag (τ), the amount which one of the signals is shifted relative to the other, at which they are most similar. The cross-correlation of two signals a and b, C_a,b, is a function of time lag, and is commonly defined as:

A useful way to understand the role of cross-correlation in SNI is that it highlights the traveltimes of seismic waves. A wavefield which has travelled between two stations will cause a similar signal to be recorded at each, shifted in time: the cross-correlation function (CCF) of the records will therefore contain a peak at a time lag which corresponds to the traveltime of the wavefield between the two stations (fig.2).

 

Figure 2. (a) a source of seismic energy (left) is recorded at receivers R1 and R2, causing identical signals separated by a time τ (right), corresponding to the travel time of the wavefield between the receivers. (b) the cross-correlation function of the two records, on which the traveltime is highlighted as a peak.

 

 

 

Cross-correlation is performed for positive and negative time lags, so CCFs have both positive ("causal") and negative ("acausal") parts. Oceanic noise arrives from all directions, and the noise records which are cross-correlated during SNI therefore contain energy which has travelled in both directions along an interstation path. GFs which emerge on noise cross-correlation functions (NCFs) will therefore contain energy in both the causal and acausal parts, symmetric about zero time lag: the causal part representing energy arriving at station B in response to an impulsive source at station A, and the acausal part energy arriving at station A in response to a source at station B (fig.3). Because GFs are usually assumed to be the same in both directions along a path, the two sides of an NCF can be treated as representing exactly the same information, but reversed in time. In reality NCFs will be perfectly symmetrical only if noise arrives from both side of the interstation path with equal strength, which is rarely the case in practice (see cross-correlation section in part 2.)

 

Figure 3. Causal and anticausal parts of an NCF. (a) Idealised NCF for the cross-correlation order station A to station B. The arrows indicate the energy path which is represented by the positive and negative parts of the cross-correlation function. (b) Representation of the noise sources which (theoretically) contribute to the causal and anticausal part of the station A - station B NCF.

 

 

Despite this potential drawback, since the first successful application of SNI in 2004 (Shaprio and Campillo (2004)) it has been consistently demonstrated that energy corresponding to the surface wave component of interstation GFs can be at least partially reconstructed using SNI. Furthermore, it has been shown that this surface wave energy can be used to infer useful information about the Earth's subsurface properties, with the same accuracy as "traditionally" used earthquake observation methods (Stehly et. al. (2007)). SNI may be of particular use in the field of volcano seismology, as recent studies have shown that it allows the detection of very small variations in seismic velocity at high temporal resolution, and that trends in these variations may correlate with some volcanic eruptions (Brenguier et. al. (2008)).

Seismic noise interferometry is still in its infancy, and it is still not completely understood what factors affect the extent to which GFs can be reproduced using the method. However, SNI represents a powerful new tool for Geophysicists, as it allows the creation of multiple, highly repeatable synthetic sources, using only the naturally occurring background seismic noise as a true source. That SNI does not require an earthquake source represents a major advantage over other seismological methods. 

2. Current work - method

As part of my ongoing MRes research at the University of Leeds (due for submission in August 2010), I perform SNI using several weeks of continuous 3-component broadband seismic records from six stations in the Montserrat Broadband Network, Montserrat, West Indies (station map available here). Data were provided by the British Geological Survey in SEISAN format, and by the Montserrat Volcano Observatory in SEISLOG format.

Using the "wavetool" and "os9sei"programs included in the SEISAN seismic analysis software, data are first converted into SAC (Seismic Analysis Code) binary format, and all further processing conducted using the SAC analysis software.

The SAC commands used for each of the following processing steps are provided in bracketed italics, and examples of their use provided. All of the steps can be easily applied to multiple files using SAC macro scripting. For a more complete explanation of the use of macros and each processing operation I refer the reader to SAC's inbuilt help section, however all of the following processing steps are also implementable using most other common seismic analysis software.

Figure 4. Diagram outlining the main steps involved in the implementation of SNI.

Raw data pre-processing

The main processing that I apply during SNI is outlined in figure 4. In the literature the exact processing steps often differ, however cross-correlation is always applied, while filtering and normalisation and/or whitening are common. Different frequency ranges may be chosen depending on the interstation distance: for example lower frequencies are more prominent on the NCFs of longer station pairs. 

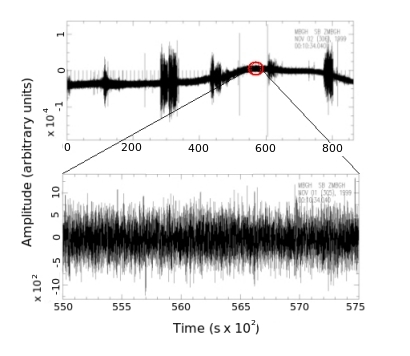Figure 5. Top: example of a 24h seismic record; note the periodic high amplitude events. Bottom: enlargement of the section contained within the red circle highlighting the background noise signal; note the order of magnitude reduction in the amplitude.

Records are initially in 20 minute segments, which I first concatenate ("merge filename") into 1 day records (Figure 5). Highly energetic events are undesirable in SNI, as only the lower amplitude ambient noise signal provides the required coherent source wavefield. As such, the data are processed to reduce the effect of larger amplitude events before cross-correlation is applied:

1. The mean and trend are removed from the data ("rmean" and "rtrend" respectively).

2. The data are high pass filtered at 0.5Hz ("hp corner 0.5"). This frequency pass is used after Sens-Schönfelder and Wegler (2006), who perform SNI in a similar location and with similar interstation distances.

3. Spectral whitening (flattening) is applied to reduce the effect of highly energetic frequencies in the records ("whiten"). 

4. In order to further down-weight the contribution of high-energy arrivals which could obscure the lower amplitude ambient noise signal, a "one-bit" normalisation is applied after various authors (e.g. Stehly et. al. (2007)) : each data point is replaced with either a 1 or -1, depending on its sign, thereby removing amplitude information from he records completely. One-bit normalisation is achieved by dividing each 24h record ("divf filename") by their absolute value ("abs"). 

Example: pre-processing of a data file

SAC> rmean                     removes the datapoint mean                  

SAC> rtrend                     removes the datapoint trend              

SAC> hp c 0.5                   high-pass filters at 0.5Hz                

SAC> whiten                     applies spectral whitening

SAC> write over                writes changes to file

SAC> read file                         

SAC> abs                          computes absolute value of processed file

SAC> write file.abs             writes absolute value to new file

SAC> read file                   reads original processed file

SAC> divf  file.abs             divides file by its own absolute value

SAC> write file.1-bit           writes one-bit normalised file

Cross-correlation

The central step in SNI is the cross-correlation of pairs of ambient noise records made at different locations. Processed 24h records are next cross-correlated ("correlate") for all possible station pair combinations. Only the vertical (Z) component is used in this first stage, so that NCFs are expected to retrieve the vertical component of Rayleigh waves, whose particle motion is confined to the vertical-radial plane. Reverse interstation paths are not computed, so that the cross-correlation order BY-GB is performed but GB-BY is not, allowing a total of 15 station pairs for the 6 stations used. 

For all station pairs with Z-Z NCFs of sufficient quality (see "assessment criteria" section), NCFs are computed for the other component pair corresponding to Rayleigh wave particle motion with a vertical component: Vertical-Radial (ZR). Reverse component pairs are not computed, so that BYZ-GBR is performed, but BYR-GBZ is not. While Love wave energy (particle motion in the transverse plane only) has been successfully retrieved using SNI (e.g. Stehly et. al. (2007)), it has not yet been studied in the current work.

Horizontal records are provided in Cartesian (NS-EW) coordinates, and it is therefore necessary to perform an appropriate rotation, into the station pair radial direction, in order to observe the non-vertical components of Rayleigh wave motion on NCFs. This is achieved by computing NCFs for the component pairs vertical-north (ZN) and vertical-east (ZE), and rotating them ("rotate") to the angle which minimises the energy on the ZE NCFs. The ZN NCF which corresponds to a minimised ZE NCFs is then defined as the ZR NCF. 

It has recently been shown (Roux (2009)) that in areas where oceanic noise is strongly directional, significant energy may be observed in NCFs where none is expected (e.g. on vertical-transverse (ZT) NCFs). By rotating the records to the direction of the oceanic noise, it was shown that this effect could be partially removed. The method of determining the ZR component on the basis of ZT energy minimisation as opposed to simply rotating the horizontal components to the interstation great circle path is chosen for this reason.

Finally the one day NCFs are stacked ("addf filename") over the whole time period (Oct 01-14-Nov 02-13 1998, Nov 01-15 1999).

Example: Cross-correlation of two processed records

SAC> correlate                               performs auto- and cross-correlations

SAC> write dummy file1-2.cc            writes the output to two files*

* For two files a and b are read into SAC's memory, the "correlate" command outputs two files: the firstly the autocorrelation of a (not used in this application), which in the above example is stored as a "dummy" variable, and secondly the desired cross-correlation of a with b. 

Assessment criteria

The quality of the computed NCFs are assessed primarily on the basis of their signal to noise ratio (SNR), that is, the ratio of the amplitude of any emerging coherent signal to that of the incoherent background signal (fig. 6). A further assessment criterion used is the coherency between 24h NCFs: while individual NCFs may stack coherently, day to day variation can be significant. This coherency analysis also allows easy identification of individual NCFs which are of poor quality, such as the bottom NCF in figure 7. It is commonplace in the literature (e.g. Brenguier et. al.) to perform running averages of days to weeks in order to stabilise NCFs over time. 

Figure 6. Two full NCF stacks (vertical-vertical component). Top: High signal to noise ratio; bottom: low signal to noise ratio

Figure 7. Twenty 1 day vertical-vertical NCFs for station pair GB-RY, exhibiting long-term coherency. The green horizontal line indicates a gap of almost 1 year, from 13th November 1998 to 1st November 199.

Of the 15 possible station pairs, only four were deemed of sufficient quality to use for further processing: GB-RY , GB-MH , GB-BY and GH-RY. Click on each to view the stacked ZZ and ZR NCFs for each.  

Identifying surface wave energy

In order to verify that any coherent energy which emerges on NCFs does in fact represent surface waves, various tests can be applied. The following examples use only the side of the NCFs (causal or acausal) with the highest amplitude, although the two sides could alternatively be averaged to increase signal to noise ratio (e.g. Sens-Schönfelder and Wegler (2006))

Particle motion

In the vertical-radial plane, the particle motion of Rayleigh waves is retrograde elliptical in solids, and this can be used as a diagnostic for their presence. Particle motion is computed ("plotpm") between the ZZ and ZR, and between the ZZ and ZT NCFs for each of the four high quality station pair. The latter pair is included as a further diagnostic for the presence of surface wave energy, since Rayleigh waves have no particle motion in the Z-T plane. The time windows over which particle motion is calculated are chosen to include prominent energy on both the Z-Z and Z-R NCFs. 

Strongly elliptical particle motion was observed for two of the four high quality NCFs. Figure 8 shows an example of a particle motion computation for one, station pair BY-GB; the other, the results for the other, GB-MH, can be viewed here.  The station pairs GB-RY and GH-RY do not show strongly elliptical motion.

Figure 8. Particle motion plot of a 15 day stacked NCF for station pair GB-BY. It shows that motion is restricted mainly to the Z-R plane, where it exhibits the eliptical motion characteristic of Rayleigh waves. (a): from top to bottom, ZZ, ZR and ZT NCFs. (b) vertical-radial, and (c) vertical-transverse particle motion during the time window within the black horizontal lines, as implied by the ZZ and ZR, and ZZ and ZT NCFs respectively.

Velocity estimation

A crude estimate of the velocity of the (assumed) surface wave energy can be made using the interstation distance, and the time lag at which the amplitude of an NCF is maximum; in the literature however, it is common to compute dispersion curves to determine velocity more accurately over a range of frequencies (e.g. Shapiro and Campillo (2004)).

Spectrograms ("spectrogram"), signal amplitude plotted as a function of time and frequency, allow the time lag of the peak amplitude to be easily determined: in the current work, all coherent energy on NCFs is confined to time lags of less than ±20 seconds, and peaks occur between around 4 and 7 seconds. Taking into account interstation distances (which range from 4-9 km) these times correspond to interstation velocities of between 0.8 and 1.3km/s (e.g. fig. 9), consistent with velocities obtained by a similar study (Baptie (2010)). The peak energies on ZZ and ZR NCFs are typically separated by a few tenths of a second (also highlighted in the particle motion plots), which is consistent with elliptical particle motion at frequencies of ~0.5Hz. 

Figure 9. Spectrogram for the ZZ component NCF for station pair RY-GH: note the peak energy of around 0.5Hz arriving at 5 seconds time lag. The interstation distance is 6.3km, indicating a peak energy velocity of around 1.25km/s.

References:

Aki, K. and Richards, P. Quantitative Seismology. University Science Books (2002).

Baptie, B.J. Lava dome collapse detected using passive seismic interferometry. Geophysical Research Letters, (2010) 37

Brenguier, F. Shapiro, N.M., Campillo, M., Ferrazzini, V., Duputel, Z., Coutant, O., and Nercessian, A. Towards forecasting eruptions using seismic noise. Nature Geoscience (2008), 1, 126-130.

Roux, P. Passive seismic imaging with directive ambient noise: application to surface waves and the San Andreas Fault in Parkfield, CA. Geophys. J. Int. (2009) 179, 367–373

Sens-Schönfelder, C., and Wegler, U. Passive ininterferometry and seasonal variations of seismic velocities at Merapi Volcano, Indonesia. Geophys. Res. Lett. (2006), 33. 

Shapiro, N.M. and M. Campillo, Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise, Geophys. Res. Lett. (2004), 31.

Stehly, L.,  Campillo, M., and Shapiro, N.M. Traveltime measurements from noise correlation: stability and detection of instrumental time shifts. Geophys. J. Int. (2007) 171 223-230.

Wapenaar, K. Retrieving the elastodynamic Green's function of an arbitrary inhomogeneous medium by crosscorrelation. Physical Review Letters (2004) , 93.